Would I Have Survived the Titanic?
Using k-Nearest Neighbors to determine if I would have survived the Titanic and make a webapp for others to use.
Project details
Project Requirements
- Clean and prepare data
- Perform exploratory data analysis
- Train a k-nn model and enter my own data
- Create a webapp to let others use the model
Project Overview
In 1912, the RMS Titanic sank to the bottom of the North Atlantic Ocean. It is perhaps the most famous shipwreck. Especially since it’s one of the deadliest tragedies with a cruise ship to this date. The event became the inspiration for many artistic works in the years after. Almost everyone knows James Cameron’s movie with Kate Winslet and Leonardo DiCaprio for example.
People are interested in documenting the sinking of the Titanic. As a result, data about the occupants is available to the public for anyone to analyze. We know, among other things, their age during the voyage, passenger class and the number of family members on the ship. Most importantly, we also know whether someone survived or perished that day. When I stumbled upon this dataset, I wondered if I would’ve survived the shipwreck. With machine learning I want to create a model that classifies people into two groups: ‘survivor’ or ‘victim’. This is based on the known characteristics of each person. When I enter my own data, I should get an estimate on the group I would belong to.
Data and Preprocessing
The data I will be using comes from Kaggle1. I will use the train.csv file to train and make the model. Each passenger has multiple attributes. These can be used to determine to classify new data later on. The dataset consists of the following attributes:
- Passenger ID
- Survived or perished
- Passenger class
- Name
- Sex
- Age
- Number of spouses or sibling onboard
- Number of parents or children aboard
- Ticket number
- Fare paid
- Cabin number
- Port of Embarkation (Cherbourg, Queenstown or Southampton)
But first I take a look at the data itself. It must not contain any missing values in order to create a trustworthy model. I plotted the data to see the ratio of missing values (yellow bars) for each column in the data.
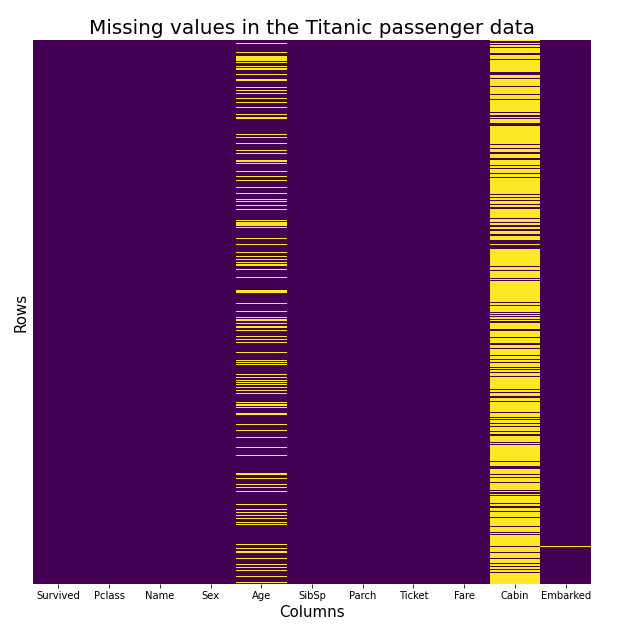
This visualization shows that three columns have rows with missing data. A number of passengers have an unknown age. I could delete this column, but something tells me this might be vital information for the model to take into consideration. I could replace the missing values with the average age (which is 30). To have a bit more variety, I took the average age of the class these people booked. The ‘Cabin’ column has too many missing values to replace, so I had to delete this information from the dataset. There is a single missing value in the ‘Embarked’ column. I dropped this single row from the data. Now there are no more omitted attributes left.
Exploratory Data Analysis
After cleaning the data, I decided to explore the dataset a little further. With some visualizations, made by Matplotlib2 and Seaborn3 for Python, survival rates for different groups became more apparent. The first plot shows the number of people that perished and lives, divided by gender.
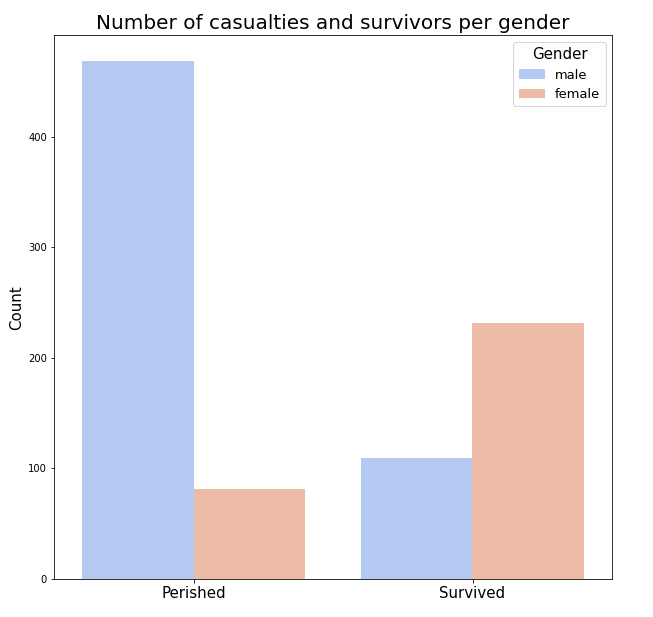
As a man, my chances of surviving the Titanic dropped significantly. Most men died in the disaster as shown by this graph. Next, I plotted the number of victims for each age group in years. (click on the plot to view a larger image)
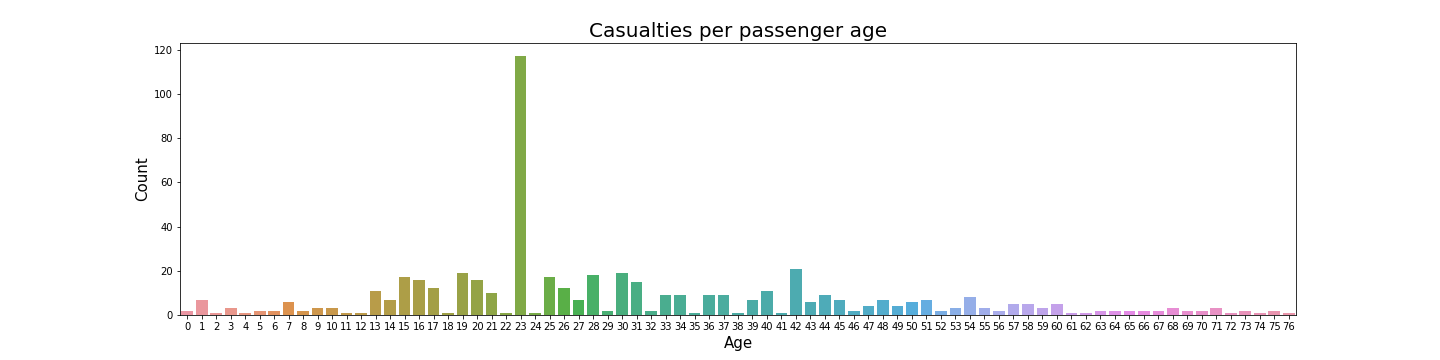
I’m 30 years of age and my chances of safely reaching the shore keep getting slimmer. Looking at this plot, I’m definitely in the group where, based on age, most people didn’t see home again.
The k-Nearest Neighbor Algorithm
There are multiple algorithms that can be used for classification tasks. For this project, I used k-nearest neighbors to calculate a model. For new data, it looks at the datapoints in its own vicinity. If the majority of it’s neighbors are part of a particular group, the new data most likely is also part of that class. The k-value stands for the amount of datapoints/neighbors that are taken into account.
A suitable k-value must be chosen to gain the best possible performance. Each value has a certain error rate, and the k with the lowest score will be chosen. One way of doing this is making multiple models, each with a different value, and plotting the results. Below is a plot with error rates for models with a k-value from 1 to 70.
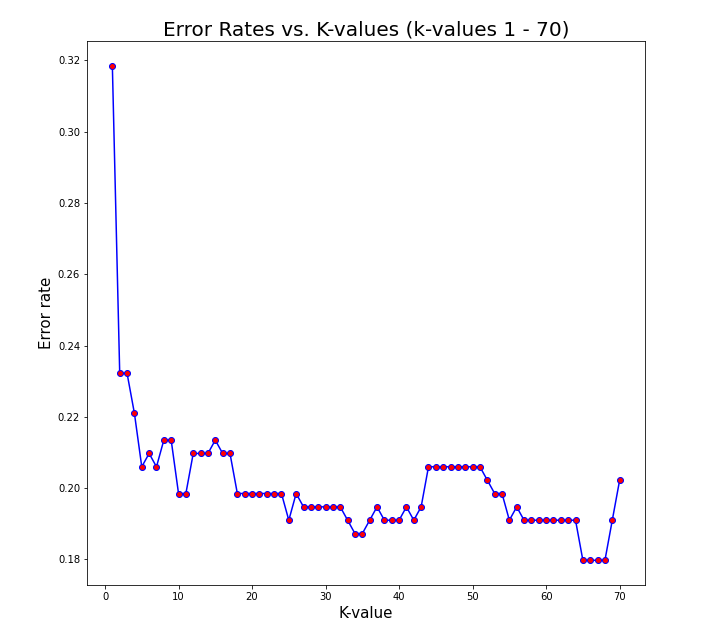
This figure shows that the lowest error rate occurs at a k-value of 63. This will be used for the model that predicts whether I would live or die. I normalized the data and split the dataset in two separate parts. One for training, and the other for testing the outcomes. After training the model, the following metrics are available to further evaluate its performance.
| Precision | Recall | F1 Score | |
|---|---|---|---|
| Died | 0.81 | 0.90 | 0.86 |
| Survived | 0.81 | 0.65 | 0.72 |
It’s easy to look at the overall accuracy of a model, but not in this case. The classes in the dataset are unbalanced since more people perished than lived. This makes accuracy a less suitable metric to rate the model. That’s why the precision and recall values are important to look at. The high precision tells me that when the model states a person died or survived, it’s probably correct. In this case, for both classes, the model is right 81% of the time. Recall quantifies the number of positive class predictions made out of all positive examples in the dataset. In this case, the model is better at capturing the data about people that died in the disaster. The F1-score shows a hormonic mean between precision and recall since it’s usually a tradeoff between the two.
Context is important in defining the appropriate metric. Since I want to minimize false positives (the model predicts I belong to the ‘died’ class while I should’ve lived), I lean more towards precision in favor of recall. So this model is most acceptable in predicting my own fate.
Would I have Survived?
With all the necessary components ready, it’s time to make a prediction about myself. I make a new entry and set my age at 30 and my gender at male. Queenstown is the closest port and is set as the port of embarkation. Next, I calculated the average fare price for each class and adjusted for inflation. A first class ticket would be €12.318,25, a second class ticket €3.079,56 and a third class ticket €2.053,03 today. These prices are calculated by adjusting for inflation in British pounds4 (average of 4.5% per year) and converting those prices to Euros. Currently, I can only afford a third class ticket and added this class and fare price (£14 back in the day) to my own data. Finally, I add zero parent or children and zero spouses or siblings. Although I would take my girlfriend with me on holiday, only married couples count in this data.
I gave this data to my model and anxiously waited for the final verdict.
drum roll..
I would have (most likely) died on the 15th of April 1912.
While not entirely unexpected after looking at the data before building the model, it's somewhat of a grim prediction. Looking at the model, it's 81% sure it picked the right group for me however.
Curious about your own chances of survival? I made a webapp that let's you use my model as well.